FOGLIO LAPIS - DICEMBRE- 2020

In questi giorni “la città alfea” si è appena apprestata a festeggiare gli 850 anni dalla nascita di uno dei suoi più illustri cittadini: Leonardo Pisano Bogollo, meglio conosciuto come Fibonacci, che sta per figlio di Bonaccio. Leonardo nasce a Pisa nel 1170 e suo padre Guglielmo è un facoltoso mercante addetto alla dogana di Bugia (oggi Béjale), in Algeria, dove la Repubblica di Pisa intratteneva fiorenti traffici commerciali. Seguendo il padre ebbe modo di trascorrere alcuni anni in Algeria orientale e di apprendere nozioni aritmetiche, sconosciute nel mondo occidentale, provenienti dal mondo indo-arabo, in particolar modo quel sistema di calcolo che basandosi su solo nove cifre ed uno zero riusciva ad indicare qualsiasi numero. Il sistema numerico decimale fu una vera rivoluzione che facilitò notevolmente l’attività contabile dei mercanti dell’epoca ancora vincolata all’uso dei numeri romani con relativa facilità di incappare in errori di interpretazione o di trascrizione.

Fibonacci è sicuramente da ritenere il più grande matematico del medioevo ed il maggior genio scientifico del XIII secolo in Italia. La sua fama era nota già ai suoi tempi a tal punto da aver trovato in Federico II un mecenate capace di apprezzare il suo talento e di comprendere la portata delle sue scoperte scientifiche. Sembra, infatti, che pur rifiutandosi di trasferirsi alla corte federiciana non è esclusa una sua certa influenza sulla progettazione di Castel del Monte. L’imperatore gli concesse un vitalizio con il quale riuscì a sostenersi continuando a studiare e a perfezionarsi.

Ma la sua scoperta più famosa è storicamente legata alla soluzione di un problema proposto proprio dall’Imperatore Federico II di Svevia durante un torneo di matematici: in un anno quante coppie di conigli si saranno ottenute da una coppia di partenza, supponendo che essa generi ogni mese, escluso il primo, una nuova coppia che a sua volta prolifica dal secondo mese? La soluzione è 144 coppie di conigli e si ottiene se ogni numero è la somma dei due precedenti per dodici mesi: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. Per la verità tale sequenza, che porta il suo nome, all’inizio non ebbe tanto successo, bisognerà attendere il 1611 quando il matematico Giovanni Keplero osservò che facendo il rapporto fra due numeri consecutivi della successione del Fibonacci esso si avvicina rapidamente per assestarsi a 1,618034. Ciò implica che nella sequenza ogni numero è più grande del precedente di un valore preciso. Tale numero irrazionale denominato phi (?), già scoperto dai pitagorici e definito da Euclide nel suo scritto gli Elementi, i greci lo avevano legato ai concetti di armonia e di bellezza. La sezione aurea o rapporto aureo o numero aureo o costante di Fidia o proporzione divina, nell’ambito delle arti figurative e della matematica, indica il rapporto fra due lunghezze disuguali, delle quali la maggiore è medio proporzionale tra l’intero segmento e la parte restante. Il numero 0,618 sta di fatto ad indicare, per convenzione, il rapporto aureo 1:1,618.

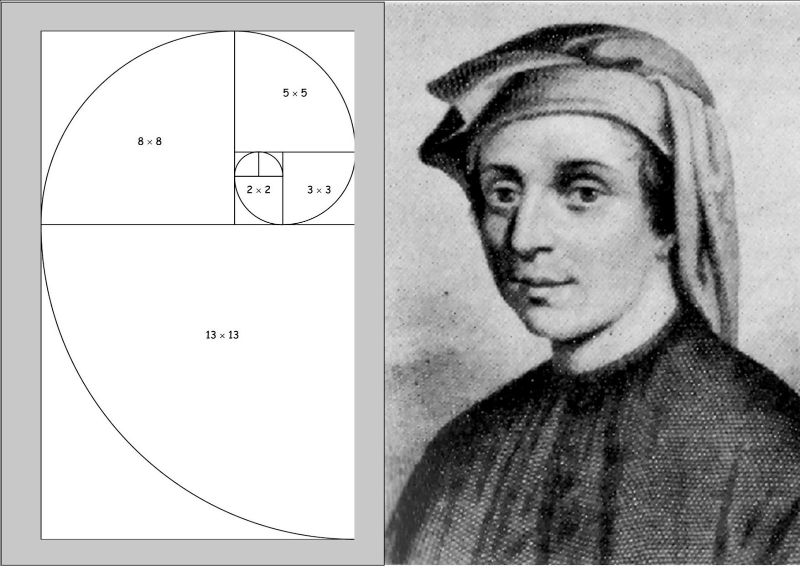
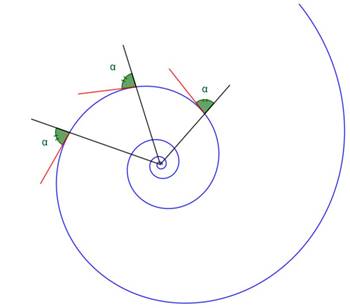
La spirale logaritmica, o equiangolare, scoperta da Cartesio nel 1638, è una figura geometrica ottenuta dalla traiettoria di un punto che si muove di moto uniformemente accelerato su una semiretta che ruota uniformemente intorno alla sua origine. La relazione esistente fra spirale logaritmica e Fibonacci consiste nel fatto che la spirale logaritmica si crea mediante l’unione di quadrati con i lati equivalenti ai numeri della successione di Leonardo, a tal punto da essere comunemente denominata spirale aurea o spirale di Fibonacci.

Se la matematica è il linguaggio della natura, come affermava Galilei, si scopre che essa è armonica e simmetrica in molti suoi aspetti. Infatti, partendo dall’osservazione e dallo studio di alcune spirali che si possono trovare in natura quali l’ordinamento delle foglie su di un ramo (fillotassi), il numero di petali di un fiore, la forma che caratterizza alcune conchiglie, il volo del falco pellegrino, etc., ci si accorge che hanno molte proprietà che li accomuna e avvicina alla successione di Fibonacci. Il rapporto aureo sembra quindi essere un importante anello di congiunzione, un punto d’incontro, tra la natura e la matematica.

Anche il corpo umano non si sottrae, basti pensare a molti punti del viso o al rapporto esistente fra la lunghezza delle falangi del dito medio e anulare o alla sezione del DNA.

Nel corso della storia numerosi sono stati gli artisti che hanno utilizzato nelle loro opere il rettangolo aureo, la cui base è la sezione aurea dell’altezza, e le forme a spirale ricavate da costruzioni geometriche da esso derivanti. Esse infatti appaiono già nelle pitture e nelle incisioni rupestri preistoriche: ne sono esempi quella ritrovata nella grotta di Oued Djerat presso Tassili-n Ajjer risalente al 6000 a.C., i motivi spiralici ad «¬S» nel mosaico dei Disegni di Nazca oltre alla costruzione delle piramidi (soprattutto quella di Cheope), al capitello ionico dell'Eretteo e in molte opere scultoree e architettoniche greche quali la facciata del Partenone di Atene.

Altri esempi si trovano nel Palazzo dell’ONU di New York e in pittura nelle opere di Vincent Van Gogh "Notte stellata" e "Autoritratto", nella "Gioconda" di Da Vinci oltre che nei suoi studi di anatomia tra cui il celebre "Uomo Vitruviano". Anche a Torino dal 2001 è possibile ammirare sulla facciata della Mole Antonelliana l’opera d’arte concettuale di Mario Merz il "Volo dei numeri" che riproduce con neon rosso i primi termini della successione di Fibonacci.
Sempre restando in campo artistico è interessante notare che Johan Sebastian Bach, Mozart, Beethoven e Schubert hanno abbondantemente inserito le proporzioni auree nei loro componimenti, ma dove si sono toccate le vette più alte è ne La sagra della Primavera di Strawinskij.

La riflessione sulla sequenza numerica scoperta da Fibonacci ci induce a pensare in modo trascendentale sul fatto che la matematica non sia mera creazione dell’uomo e che essa si sia evoluta parallelamente alla società umana, basti pensare ai babilonesi che già impiegavano il teorema di Pitagora e alla versione dell’abaco a polvere fenicio, abak, e all’uso inconsapevole del p da parte degli egizi. Forse ha ragione F. W. August Fröbel quando afferma che “la matematica si può considerare come ciò che unisce e si interpone fra l’Uomo e la Natura, fra il mondo esterno e quello interno, fra il pensiero e la percezione”.

                                                                 Clemente Porreca